Log-t distribution

In probability theory, a log-t distribution or log-Student t distribution is a probability distribution of a random variable whose logarithm is distributed in accordance with a Student's t-distribution. If X is a random variable with a Student's t-distribution, then Y = exp(X) has a log-t distribution; likewise, if Y has a log-t distribution, then X = log(Y) has a Student's t-distribution.

Characterization

The log-t distribution has the probability density function:

${\displaystyle p(x\mid \nu ,{\hat {\mu }},{\hat {\sigma }})={\frac {\Gamma ({\frac {\nu 1}{2}})}{x\Gamma ({\frac {\nu }{2}}){\sqrt {\pi \nu }}{\hat {\sigma }}\,}}\left(1 {\frac {1}{\nu }}\left({\frac {\ln x-{\hat {\mu }}}{\hat {\sigma }}}\right)^{2}\right)^{-{\frac {\nu 1}{2}}}}$,

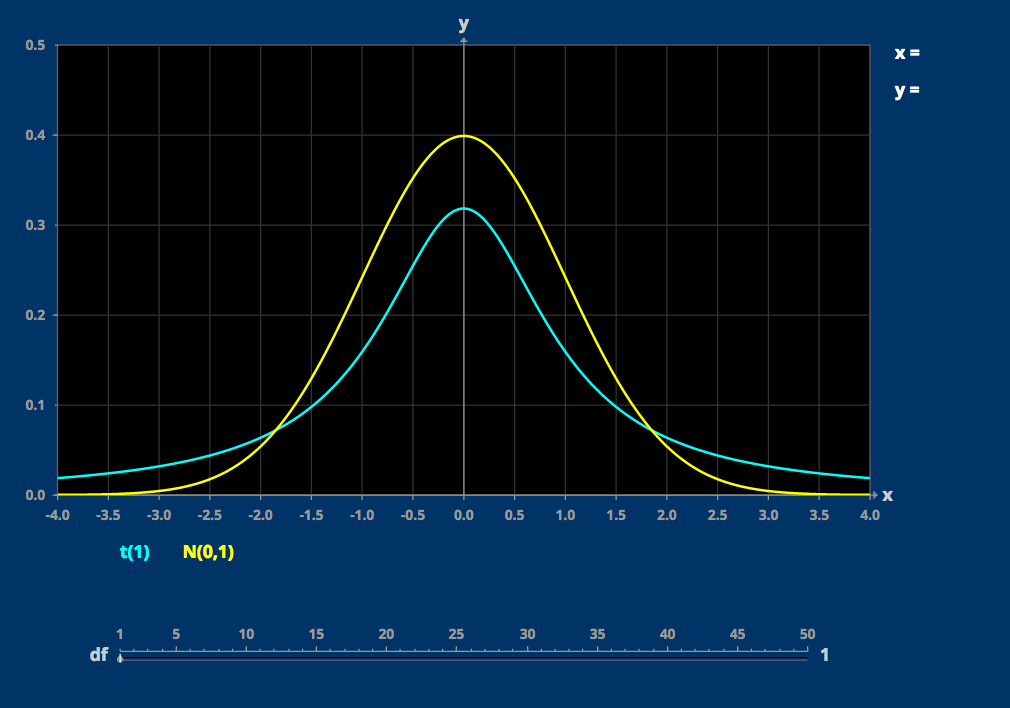
where ${\displaystyle {\hat {\mu }}}$ is the location parameter of the underlying (non-standardized) Student's t-distribution, ${\displaystyle {\hat {\sigma }}}$ is the scale parameter of the underlying (non-standardized) Student's t-distribution, and ${\displaystyle \nu }$ is the number of degrees of freedom of the underlying Student's t-distribution. If ${\displaystyle {\hat {\mu }}=0}$ and ${\displaystyle {\hat {\sigma }}=1}$ then the underlying distribution is the standardized Student's t-distribution.

If ${\displaystyle \nu =1}$ then the distribution is a log-Cauchy distribution. As ${\displaystyle \nu }$ approaches infinity, the distribution approaches a log-normal distribution. Although the log-normal distribution has finite moments, for any finite degrees of freedom, the mean and variance and all higher moments of the log-t distribution are infinite or do not exist.

The log-t distribution is a special case of the generalized beta distribution of the second kind. The log-t distribution is an example of a compound probability distribution between the lognormal distribution and inverse gamma distribution whereby the variance parameter of the lognormal distribution is a random variable distributed according to an inverse gamma distribution.

Applications

The log-t distribution has applications in finance. For example, the distribution of stock market returns often shows fatter tails than a normal distribution, and thus tends to fit a Student's t-distribution better than a normal distribution. While the Black-Scholes model based on the log-normal distribution is often used to price stock options, option pricing formulas based on the log-t distribution can be a preferable alternative if the returns have fat tails. The fact that the log-t distribution has infinite mean is a problem when using it to value options, but there are techniques to overcome that limitation, such as by truncating the probability density function at some arbitrary large value.

The log-t distribution also has applications in hydrology and in analyzing data on cancer remission.

Multivariate log-t distribution

Analogous to the log-normal distribution, multivariate forms of the log-t distribution exist. In this case, the location parameter is replaced by a vector μ, the scale parameter is replaced by a matrix Σ.

References